Circular Motion Angular Velocity and Acceleration

Angular variables:-
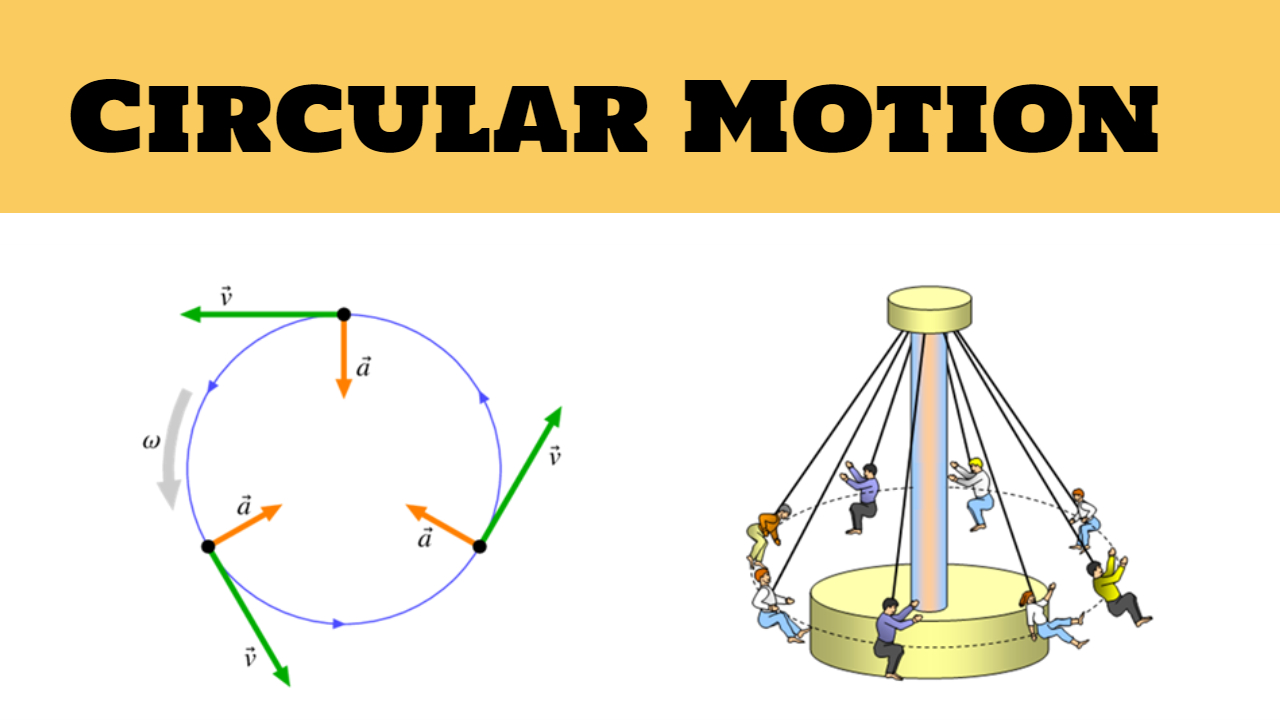
Circular motion is a two-dimensional motion or motion in a plane.

Suppose, a particle is moving in a circle of radius R and centre ‘O’, The position of particle P at a given instant may be described by the angle, this angle theta is called the angular position of the particle.

As the particle moves on the circle its angular position changes.

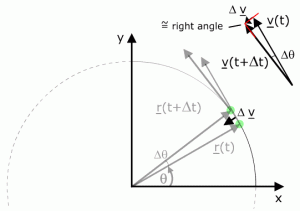
Suppose, the point rotates an angle \(\Delta \theta \) in time \(\Delta t\) the rate of change of angular position is known as the angular velocity \(\omega \).                \( \alpha \)

\( \omega =\dfrac {d\theta }{dt} \)

The rate of change of angular velocity is called angular acceleration Alpha (\( \alpha \)).

\( \alpha =\dfrac {d\omega }{dt}=\dfrac {d^{2}\theta }{dt^{2}} \)

Suppose, a particle moving in a circle of radius R then the relation between its linear and angular velocity is stabilized by this equation

\( V=r\omega \)

Due to change in angular velocity acceleration produce it’s called tangential acceleration. The relation between tangential acceleration and angular acceleration is stabilized by this equation

\( a_{t}=r\alpha  \)

or

\(a=\dfrac {dv}{dt}=r\dfrac {d\omega }{dt}=r\dfrac {d^{2}\theta }{dt^{2}}\)

Velocity and acceleration of a particle in a circular motion:-
Suppose, a particle moving in a circular path having radius r with velocity v. then following point must be noted,

• The particle has only tangential velocity.
• If the particle moves in a uniform circular motion. then its tangential velocity component doesn’t change. it means it does not produce any tangential acceleration. So, in this type of motion, only one acceleration act in the direction of the centre called radial acceleration. This acceleration is generally responsible to provide the circular motion to the particle, due to this acceleration a force provided to the particle is called centripetal force. This force is responsible to move the particle in a circular path.
• Is particle move with non-uniform velocity. it means its velocity changes with respect to time. Due to this change, an acceleration produces in the direction of velocity called tangential acceleration. In this situation, the particle having two-component of acceleration one is tangential component and another is a radial component but this two acceleration is not the total acceleration. The total acceleration is the resultant of these two acceleration. That means total acceleration always greater than this two individual acceleration.

Total acceleration is

\( \overrightarrow {a}=-w^{2}r\widehat {e_{r}}+\dfrac {dv}{dt}\widehat {e_{t}} \)

To calculate and drive tangential and radial acceleration in a circular motion, first of all, we have to assume two-unit vector along the tangential as well as in the radial direction.

These are two unit vector along the tangential and radial direction
\( \widehat {e_{r}}=\cos \theta \widehat {i}+\sin \theta \widehat {j} \)

\( \widehat {e_{t}}=-\sin \theta \widehat {i}+\cos \theta \widehat {j} \)

Tangential acceleration component

\( a_{t}=\dfrac {dv}{dt} \)

Radial acceleration component

\( a_{r}=r\omega ^{2} \)

Total Acceleration

\( a_{total}=\sqrt {a^{2}_{r}+a^{2}_{t}} \)

\( a=\sqrt {\left( r\omega ^{2}\right) ^{2}+\left( \dfrac {dv}{dt}\right) ^{2}} \)

\(  \)

To find velocity v differentiate position vector with respect to time its gives velocity.
Again to find acceleration we have to differentiate velocity with respect to time and this derivation gives us two-component of acceleration one is tangential component and another is a radial component.

Following points are important regarding the above discussion

• In uniform circular motion speed of the particle is constant that is tangential acceleration is zero and total acceleration is equal to radial acceleration and the direction of total acceleration is along the direction of the centre.
• In accelerated circular motion tangential acceleration is positive. that it’s act along the direction of the velocity vector.
  In a decelerated circular motion tangential acceleration is negative that is antiparallel to the velocity vector.